Mathematical modeling of cell fate decisions to understand cancer biology

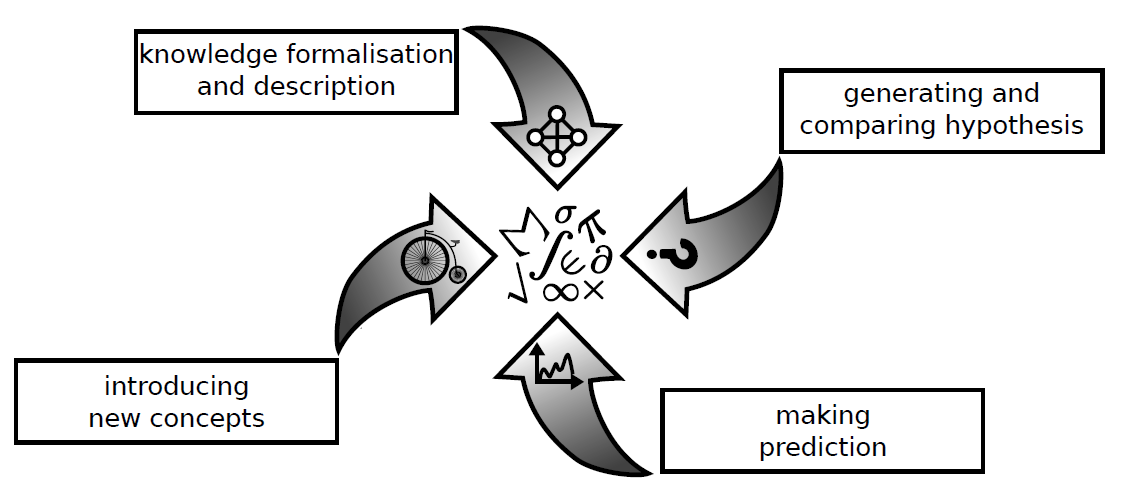
Mathematical models serve to explain complex biological phenomena and provide predictions that can be tested experimentally. They can provide plausible scenarios of a complex biological behaviour when intuition is not sufficient anymore. Mathematical models can provide the appropriate tools to interpret all sorts of experimental observations in a rigorous and systematic manner. More specifically, we propose four characteristics or hallmarks of a mathematical model:

• A model facilitates the formalisation of our knowledge: it aims at describing biological phenomena in a formal and unambiguous way; it recapitulates (integrates all facts) and summarises (provides concise description) what is known about a biological process; it allows the identification and the listing of the key players and mechanisms involved in a process; it also provides a way to visualise biological data;
• A model helps the generation and comparison of hypotheses: it enables analyses and interpretation of biological data; this leads in turn to the formulation of hypotheses on the network structure, on the plausible molecular interactions behind a process;
• A model formulates predictions: it can predict results such as mutant phenotypes, response to drug treatments, identification of therapeutic intervention points, behaviours in particular cellular contexts; it can also test and rank predictions by performing in silico experiments; it can anticipate side-effects of drugs or perturbations;
• A model enables conceptualization: it can be used as an abstract thinking object and it allows introduction of new concepts in biology: in particular it can give formal definition for a class of behaviours and cellular observations (e.g., any dynamical behaviour of individual motifs)

Over the past years, we have developed logical models that focus on cell fate decisions, cell cycle, apoptosis, EMT and migration, etc. with the purpose of understanding which mechanisms are deregulated in some particular contexts and that can lead to cancer.

Highlights